Research interests
Current research interests
Multiscale modeling
My main interest is developing methodology for data-driven bottom-up / ab initio multi-scale modeling. I’m interested in applying such approaches to hard condensed matters (mainly weakly-correlated systems) and soft matters (polymer, proteins, …).
The figure below is an overview of physical processes happening on different scales and the corresponding descriptive models. For example, for non-relativistic quantum systems, the dynamical model is the Schrodinger equation.
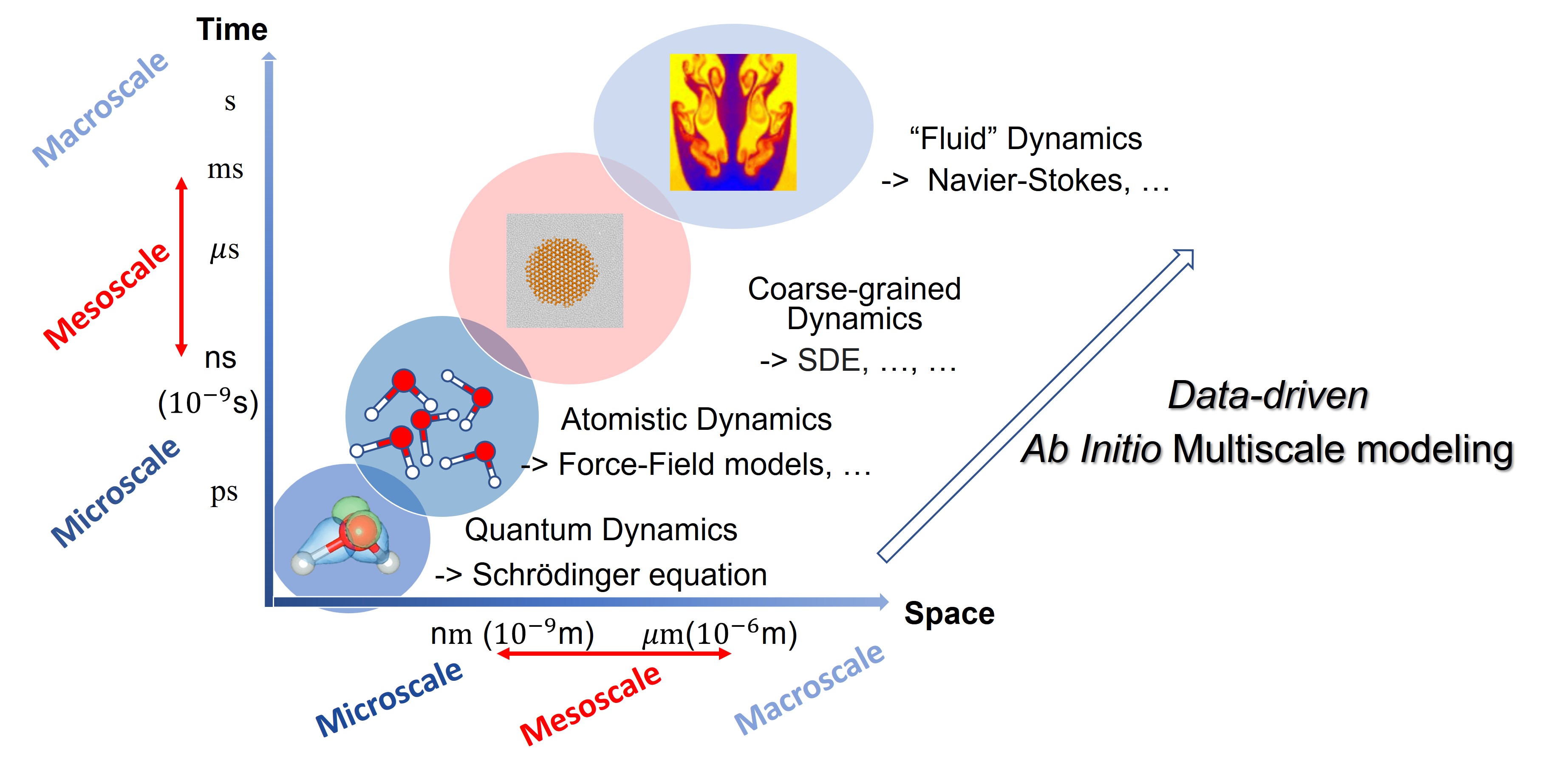
In principle, the other dynamical models (e.g. inter-atomic force field models) on higher scales can be derived from Schrodinger equation. In recent years, the development of machine learning allows us to explore this possibility. Now for many realistic materials, we are able to extract accurate atomistic models from quantum mechanical data, with appoaches like DeepMD.
Based on accurate atomistic models, one can further derive coarse-grained models describing the dynamics of collective variables defined on atomistic degrees of freedom. I developped a numerical framework, ab-initio generalized Langevin equation (AIGLE), for achieving this goal.
Publications
P. Xie, R. Car, and W. E. Ab Initio Generalized Langevin Equations
. arXiv:2211.06558 (2022).
P. Xie, Y. Chen, W. E, and R. Car. Ab initio multi-scale modeling of ferroelectrics: The case of PbTiO3. arXiv:2205.11839 (2022).
Ferroeletric material
I am interested in modeling ferroelectric materials in terms of phase transition, domain motion and quantum effects, etc.
Publications
P. Xie, Y. Chen, W. E, and R. Car. Ab initio multi-scale modeling of ferroelectrics: The case of PbTiO3. arXiv:2205.11839 (2022).
Previous Research interests
Quantum Monte Carlo
I was interested in developing machine learning-assisted quantum Monte Carlo (QMC) methods for solving ground states and simulating unitary quantum dynamics.
Publications
P. Xie, and W. E. Coarse-grained spectral projection: A deep learning assisted approach to quantum unitary dynamics. Phys. Rev. B 103.2 (2021): 024304.
R. Wu, X. Cao, P. Xie, and Y. Liu. End-to-end quantum machine learning implemented with controlled quantum dynamics. Phys. Rev. Appl. 14.6 (2020): 064020.
Spectral graph theory
My earliest research interests are in spectral theory of complex networks. I am not active in this field anymore.
Selected Publications
P. Xie, Z. Zhang and F. Comellas. The normalized Laplacian spectrum of subdivisions of a graph. Appl. Math. Comput. 286 (2016): 250-256.
P. Xie, Z. Zhang and F. Comellas. On the spectrum of the normalized Laplacian of iterated triangulations of graphs. Appl. Math. Comput. 273 (2016): 1123-1129.
P. Xie, Y. Lin and Z. Zhang. Spectrum of walk matrix for Koch network and its application. J. Chem. Phys. 142.22 (2015): 224106.
